Sensor fusion: Unterschied zwischen den Versionen
(→Sensor fusion (EKF)) |
(→Sensor fusion (Gyrodometry)) |
||
| Zeile 42: | Zeile 42: | ||
=Sensor fusion (Gyrodometry)= | =Sensor fusion (Gyrodometry)= | ||
| − | The of 'Gyrodometry' is to compare delta | + | The of 'Gyrodometry' is to compare delta phi of gyro and odometry. If it is higher than a certain threshold, use gyro delta phi, otherwise odometry delta phi. |
| − | if ( | + | if (deltaPhiGyro - deltaPhiOdo) > deltaThres |
| − | + | phi = phi + deltaPhiGyro * T | |
else | else | ||
| − | + | phi = phi + deltaPhiOdo * T | |
=Position recalibration at perimeter border= | =Position recalibration at perimeter border= | ||
Version vom 24. Februar 2015, 15:09 Uhr
Inhaltsverzeichnis
Abstract
NOTE: Everything under development here. Just showing ideas! :-)
The actual state of the robot can be described completely by:
- speed (m/s)
- direction (degree)
- position (x,y - meter)
All sensors (gyro, acceleration, compass, odometry, perimeter signal strength, GPS, ...) can deliver certain information about the robot's state. However, each sensor is noisy (added with errors). Sensor fusion is used to eliminate errors of each individual sensor. Each sensor gets a confidence weight that is automatically adjusted after reading the sensor by comparing its plausibility with the fusion result.
Sensor errors
- Odometry: accumulation error (e.g. 15cm per meter), update rate: 10-20 Hz
- Gyro: accumulation error (e.g. 0.03 degree per second), update rate: 10-20 Hz
- Compass: noise (e.g. 1 degree), update rate: 10-20 Hz
- GPS: noise (e.g. 2m), update rate: 1-5 Hz
Odometry sensor error
After a time, the odometry's error accumulates, and the course (Degree) and position (x/y) are getting unprecise.
Typical errors in outdoor condition (wet lawn, high slope):
- Distance: 20cm per meter
- Course: 10 degree per meter
The course can be permanently corrected by the compass sensor, the position by recalibration on the perimeter wire.
Sensor fusion (EKF)
A Kalman or Extended Kalman Filter (EKF) filter can be used for sensor fusion. Sensor fusion helps improving precision of course and distance measurements by fusion of all available sensors.
Gyro => Rotation speed delPhi => Course(GPS) => Course phiGPS => Kalman => Course phi => Odometry => Distance Sl, Sr => Kalman => Position x,y, Course phi
Note: This estimated position will need to be corrected by an absolute position estimation, e.g. perimeter field strength (and a particle filter) or position recalibration at perimeter border.
Sensor fusion (Gyrodometry)
The of 'Gyrodometry' is to compare delta phi of gyro and odometry. If it is higher than a certain threshold, use gyro delta phi, otherwise odometry delta phi.
if (deltaPhiGyro - deltaPhiOdo) > deltaThres phi = phi + deltaPhiGyro * T else phi = phi + deltaPhiOdo * T
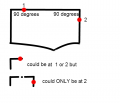
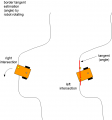
Position recalibration at perimeter border
Because odometry error increases over time, the robot needs to periodically recalibrate its exact position (get the error to zero). This works by detecting its exact position on the perimeter wire (using cross correlation).
- Learn mode: robot completely tracks perimeter wire once and saves course (degree) and distance (odometry ticks) in a list (perimeter tracking map).
- Position detection: robot starts tracking the perimeter wire at arbitrary position until a high correlation with a subtrack of the perimeter tracking map is found. There it can stop tracking and knows its position on its perimeter tracking map.
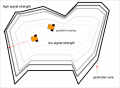
Mapping and localization (SLAM)
The perimeter magnetic field could be used as input for a robot position estimation. However, as both the magnetic field map and the robot position on it is unknown, the algorithm needs to calculate both at the same time. Such algorithms are called 'Simultaneous Localization and Mapping' (SLAM).
Input to SLAM algorithm:
- control values (speed, steering)
- observation values (speed, heading, magnetic field strength)
Output from SLAM algorithm:
- magnetic field map (including perimeter border)
- robot position on that map (x,y,theta)
Example SLAM algorithms:
- Particle filter-based SLAM plus Rao-Blackwellization: model the robot’s path by sampling and compute the 'landmarks' given the poses
Example implementation: The idea is to use a particle filter that constantly generates a certain amount of 'guesses' (particles, e.g. N=50) where the robot can be (depending on the last position, control input, speed sensor and heading sensor measurements). Each 'particle' is evaluated by the perimeter field measurement...
... and the particle 'weight' is adjusted based on that. Bad particles are replaced by new particles with new guesses near the good guesses. This constantly produces particles with high probability of the robot's location.
SLAM simulation
- The simulator code can be found in SVN
- The simulator IDE+compiler+precompiled libs (CodeBlocks) can be downloaded here - Extract the .zip to 'C:\codeblocks' and run 'sim.cbp'
Videos:
Magnetic field localization using particle filter
Lane-by-lane mowing
In the lawn-by-lane mowing pattern, the robot uses a fixed course (accurate gyro + compass correction). When hitting an obstacle, the new course is added by 180 degree, so that the robot enters a new lane.
The robot always starts at the borders at an arbitrary choosen course, mowing lane by lane of a maximum length (distance determined by odometry). The maximum length ensures that the odometry position error does not get too high. At the perimeter, the robot can reduce the error to zero again (one axis). The arbitrary starting course ensures that even small gaps on the lawn are mown completely after a 2nd mowing session (where the robot started at another arbitrary course).
The maximum allowed yaw error (course error) can computed like this:
yaw error=arcsin(lane width error/lane length)
Assuming a lane length of 10m, and a lane width error of +/- 0.1m, the maximum allowed yaw error is:
yaw error=arcsin(0.1m/10m) = 0.5 degree
Assuming that robot moves at 0.4m/sec, the actual yaw error can be computed like this:
actual time needed = 10 meters / 0.4m/sec = 25 seconds
Actual yaw error (assuming gyro noise 0.005 degree/sec):
actual yaw error = 0.005 degree/sec * 25 seconds = 0.125 degree
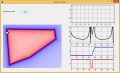
Simulation
Here's [1] a simulation of localization using odometry sensors.